Història de Pitàgores (II)

Nombres irracionals:

Els pitagòrics consideraven que qualsevol fenomen de l’univers es podia explicar mitjançant els nombres enters i els seus quocients.

Defensaven que el món era “harmonia i nombres” i que tot s’ordenava segons proporcions.

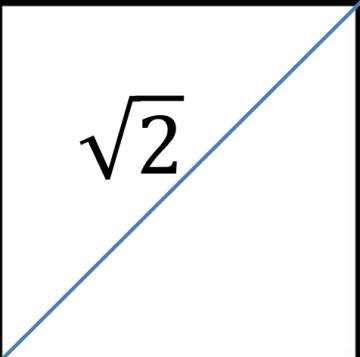
Però, com a conseqüència del Teorema de pitàgores, van veure que no hi havia cap manera d’expressar el valor de la longitud de la diagonal d’un simple quadrat. Cap operació aritmètica ni cap fracció podia donar el seu valor, en funció de la longitud A del costat. Així, van descobrir que existien uns altres nombres que no es podien posar en forma de fracció, i els van  anomenats els “incommensurables” o “irracionals”.

La situació va ser realment dramàtica. Tan dramàtica, que van decidir mantenir en secret la demostració. Era difícil acceptar que havien demostrat la falsedat del seu propi mite. Havien trobat un resultat estrany, irracional. Per això, els nombres que mesuren magnituds com la diagonal d’un quadrat o la superfície d’un cercle que no es poden expressar com fraccions, se’ls anomena nombres irracionals. Les matemàtiques dels irracionals van nàixer de la perplexitat dels pitagòrics.

Curiosament, el pentagrama o estrella de cinc puntes que era el símbol dels pitagòrics conté el nombre auri, un nombre irracional.

Els segments acolorits del pentagrama tenen proporcions àuries