Relacions entre els elements d'un triangle

Aquestes relacions són molt importants per la resolució de problemes de geometria plana, ja que gràcies a elles, és possible determinar mesures desconegudes d'angles i costats.

Relacions entre els costats d'un triangle

Donat un triangle ABC, sempre es compleix que:

• Qualsevol costat és menor que la suma dels altres dos.

\( a < b + c\)

\( b < a + c\)

\( c < a + b\)




• Qualsevol costat és major que la diferència dels altres dos.

\( a > b - c\)

\( b > a - c\)

\( c > a - b\)

Exemple:
Comprova si els següents segments formen un triangle:

• \(a = 2\)  cm,  \(b = 3\) cm,  \(c = 4\) cm:

\( 2 < 3 + 4\)

\( 3 < 2 + 4\)

\( 4 < 2 + 3\)



Aquests tres segments si que poden formar un triangle.


• \(a = 1\)  cm,  \(b = 2\) cm,  \(c = 3\) cm:

\( 1 < 2 + 3\)

\( 2 < 1 + 3\)

\( 3 < 1 + 2\)



Aquests tres segments NO poden formar un triangle.

Relacions entre els angles d'un triangle

La suma dels tres angles d'un triangle sempre és 180º.

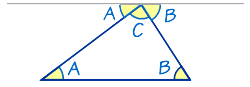
Si tracem una recta paral·lela al costat c que passe pel vèrtex oposat C, es formen dos angles equivalents a A i B. Com que la suma dels angles és un angle plà, \(A + B + C = 180º\).